数值地球
2025-09-16
绪论
0.1 数值方法在地球科学中的重要性
地球科学是研究地球系统各组成部分及其相互作用的综合性学科,涵盖大气科学、水文学、地质学、地貌学、环境科学等多个领域。随着科学技术的不断发展和计算能力的快速提升,数值方法已成为现代地球科学研究中不可或缺的重要工具。
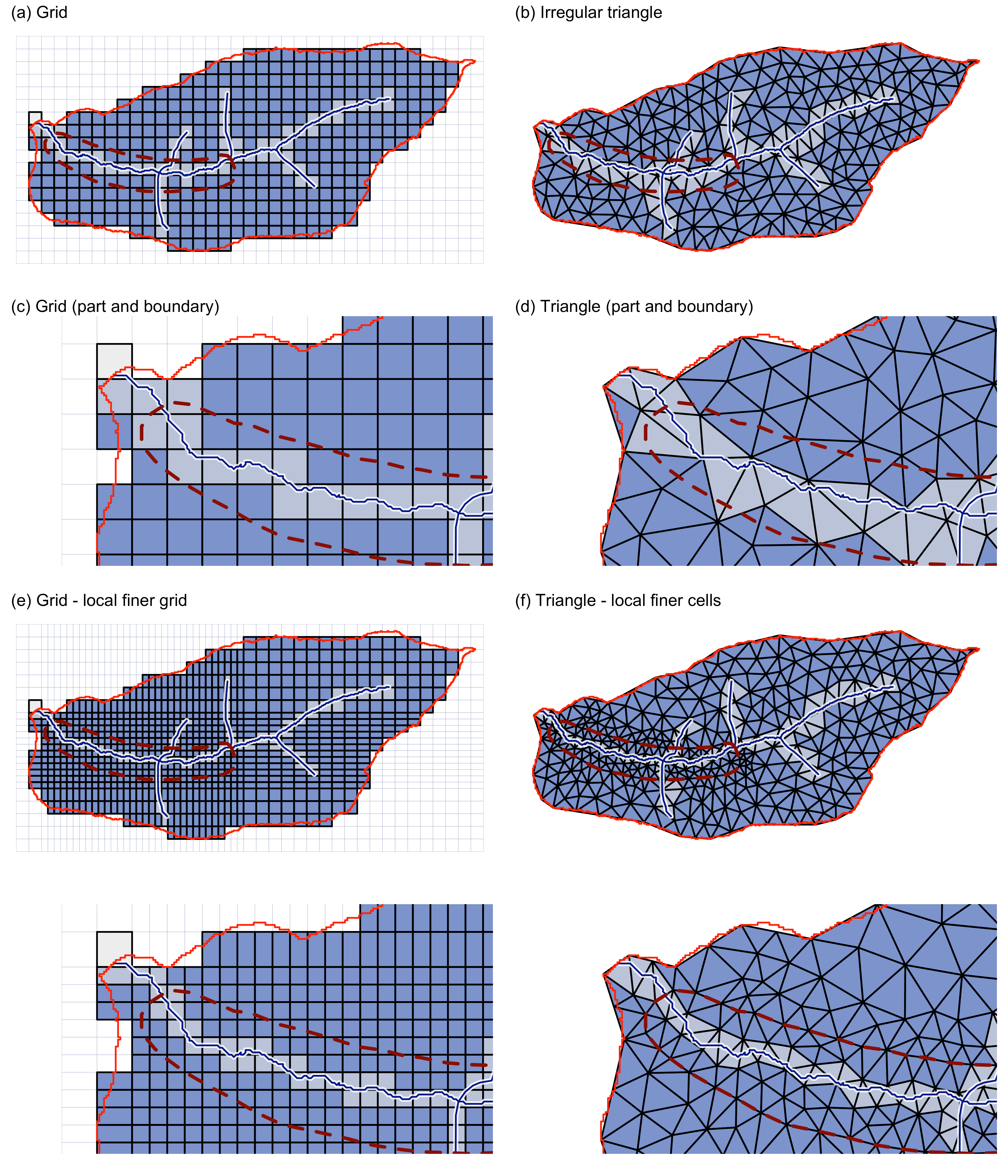
数值方法在地球科学中的应用
数值方法通过将复杂的物理过程转化为数学方程,并利用计算机进行数值求解,使我们能够:
- 模拟复杂的地球系统过程:从大气环流到地下水流动,从冰川运动到地震波传播
- 预测未来变化趋势:气候变化预测、洪水预报、地震预警等
- 优化资源管理:水资源配置、环境治理、灾害防控等
- 验证理论假设:通过数值实验验证科学理论的有效性
0.2 本书的目标与特色
本书旨在为地球科学领域的学生、研究人员和工程师提供一套系统、实用的数值方法教材。我们采用理论与实践相结合的方式,通过丰富的代码示例和实际应用案例,帮助读者:
- 掌握数值方法的基本原理:理解各种数值方法的数学基础和适用条件
- 学会编程实现:使用R语言实现各种数值算法
- 解决实际问题:将数值方法应用于具体的地球科学问题
- 培养计算思维:提高利用计算机解决科学问题的能力
0.3 主要内容概览
本书共分为六个主要章节,内容安排如下:
0.3.1 第一章:建模基本方法论
介绍CLAMS方法(概念模型、物理定律、假设、数学公式、求解器),这是将现实世界问题转化为可计算数学模型的标准流程。详见??。
0.3.2 第二章:数值方法基础
讲解显式与隐式求解法、数值迭代方法等基础概念,为后续章节的学习奠定基础。详见??。
0.3.3 第三章:有限差分法
详细介绍泰勒级数展开、差分格式构造、稳定性分析等有限差分法的核心内容。详见??。
0.3.4 第四章:有限元法
深入探讨变分原理、形函数理论、单元矩阵构造等有限元法的理论基础和实现方法。详见??。
0.3.5 第五章:有限体积法
系统介绍控制体积、通量计算、离散化方程等有限体积法的关键概念。详见??。
0.3.6 第六章:应用案例
通过大气科学、水文学、地质学、环境科学等领域的实际案例,展示数值方法的具体应用。详见??。
0.4 学习建议
为了更好地学习本书内容,建议读者:
- 具备必要的数学基础:微积分、线性代数、常微分方程等
- 熟悉R语言编程:本书所有代码示例均使用R语言实现
- 动手实践:认真完成每章的练习题和编程作业
- 理论联系实际:将所学方法应用到自己的研究领域
0.5 代码示例:简单的数值积分
让我们通过一个简单的例子来感受数值方法的魅力。考虑计算定积分:
这个积分没有解析解,但我们可以用数值方法近似计算:
# 使用梯形法则进行数值积分
trapezoidal_rule <- function(f, a, b, n) {
h <- (b - a) / n
x <- seq(a, b, length.out = n + 1)
y <- f(x)
return(h * (sum(y) - 0.5 * (y[1] + y[length(y)])))
}
# 定义被积函数
f <- function(x) exp(-x^2)
# 计算积分值
result <- trapezoidal_rule(f, 0, 1, 1000)
cat("数值积分结果:", result, "\n")
cat("与精确值比较:", abs(result - 0.7468241), "\n")
# 可视化积分过程
library(ggplot2)
x_plot <- seq(0, 1, length.out = 100)
y_plot <- f(x_plot)
df <- data.frame(x = x_plot, y = y_plot)
ggplot(df, aes(x = x, y = y)) +
geom_line(color = "blue", size = 1) +
geom_area(fill = "lightblue", alpha = 0.3) +
labs(title = "数值积分示例:∫₀¹ e^(-x²) dx",
x = "x", y = "f(x) = e^(-x²)") +
theme_minimal()这个简单的例子展示了数值方法如何帮助我们解决看似复杂的问题。在后续章节中,我们将学习更多高级的数值方法,并探索它们在地球科学中的广泛应用。